In this post I will describe a method to visualize motion in 4D space by way of thought experiments.
This proposes an informal technique I use and the pitfalls I’ve fallen into, it’s not a rigorous article about 4D geometry. I find this visualization framework useful and it served as a stepping stone to get a much more organic understanding of hypersolids. Hopefully this helps someone else as well.
This actually started as a tutorial on how to gain intuition into some of the regular 4D polytopes, based on the 16-cell. During the course of writing I realized that 4D space navigation and 4D figure visualization were sufficiently different in terms of abstractions and insight requirements that they would be better handled separately.

"I am simply out of Lineland, that is to say, out of the Straight Line which you call Space,
and in the true Space, where I can see things as they are".
-- Flatland.
Introduction
Objective & scope
The primary objective is that by the end of this post you should have expanded your mental toolkit and be more comfortable with 4D euclidean space. Mainly, being able to better think about where all the space is.
Rationale
We can view the grand space of possible ideas as an immense, mostly uncharted field, and one has to reach certain spots in order to be able to think certain thoughts. There seems to be an undiscovered continent of insights laying behind the 4D blockage. We ought to manipulate 4D space and 4D objects as first class concepts, leverage that to reach new grounds, and have a look at what we can see from over there.
4D data types are encountered in engineering. For myself two unrelated problems renewed my curiosity of 4D geometry a few years ago: performing rotations in space using quaternions and parameterizing incoming light rays to characterize light fields. One does not need to be a math guru to like an abstract thinking challenge 🙃.
Most people take for granted that, as 3D beings, it must not be possible to even conceive of 4D space or 4D figures. I like to consider that humans are akin to visually impaired 4D beings: we might not need to see the World with external senses to be able to visualize it internally. See for instance Bernard Morin, a blind mathematician who contributed crucial insights in topology. In higher dimension, Alicia Boole Stott, an amateur with no formal mathematical training, taught herself to visualize 4D space and contributed several early results to the field without using analytical geometry. She built models of the 3D cross sections of all the 4D regular polytopes. Some of them are shown in fig. 2.

Fig. 2. Perpendicular cross sections of the 600-cell, created by Alicia Boole Stott circa 1890.
Stay away from projections
Misleading tesseracts
In Fig. 3. you can see the classic “nested cubes” representation of the tesseract. I hate how ubiquitous this representation is, how it has become a synonymous of the tesseract itself. It makes things much more complicated than they really are, it’s full of mystique, especially the rotating versions, and it’s very confusing.
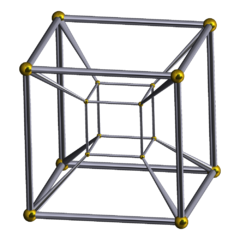
Fig. 3. Not really a tesseract.
The core idea behind this image is the concept of a 4D camera, a camera that takes pictures in 4D space and capture them on a 3D sensor. The imaged object becomes a 3D shape sitting in a standardized volume.
The insights are blocked behind the cognitive load of how the 4D perspective camera is projecting the objects onto its volumetric sensor. You would need to deeply grok the 4D camera first in order to even appreciate the shortcomings of the image.
For example, using this perspective projection as a visualization support I think it’s almost impossible to realize that there are points inside the tesseract that are not inside any of the eight cubes visible in the image, or that if you trace a diagonal between the corners of the tesseract you do not pass through any of the eight cubes.

Fig. 4. Not really the Venus de Milo.
Non content with projecting 4D to 3D, we go further and double project down to 2D. You are now working with the shadow of a shadow. Fig. 4. shows the Venus de Milo, a 3D object, projected down to 2D and then to 1D: not as impressive as the original.
Not much better in VR
What if we can experience the 3D “image” first hand? It gets slightly better in VR or with a stereoscopic display and there are hints you can add like color, size or removing some faces, but in the end it still makes for poor learning material in my opinion. I still view it as a toxic meme.
In 2016 as a side project I implemented a 4D camera in Unity and placed myself in VR inside the projection of a tesseractic honeycomb, thinking it would provide me with new insights. It was a failure: the only enlightenments I got were from writing the code for the camera in the first place, not from the VR experience.
Misleading perspective
Due to the perspective projection, the nested cubes representation is also not necessarily the projection of a tesseract anyway. There are many 4D shapes that could create this result. For instance the cell further away from the camera on the W axis could be very far and correspondingly very big, and you would get the same 3D object. It’s the same issue we have when viewing the perspective projection of a 3D object on a 2D image, something might look like a cube or a cylinder, but it could very well be something else.

Fig. 5. Ambiguous Cylinder and a mirror by Kokichi Sugihara.
Traveling in 4D
The core idea is to treat the fourth axis as a contracting/expanding sphere decoupled from regular space. Let’s see what this means.
The sphere out of this World
Let’s classically treat X, Y and Z as the familiar regular axes, and W as the fourth axis.
The core exercise is to move from point to point in 4D space. We will do this by moving in XYZ space and, independently, moving on W.
- Visualize a single point in 3D space. Let’s consider it located at the origin. You can mentally see the three axes crossing through it.
- We will lock this point in 3D, it will not move on X, Y or Z.
- Focus on the point and clear all imagery of the space around it. It’s now floating in a void. This is how we focus on the W axis independently.
- Now picture a sphere around the point. Think of the surface of the sphere as if it was covered with tiny eyes looking inward. Wherever you are on the surface, the point at the center is always one radius in front of the eye.
- In this imagery, we consider that this sphere is a second point, it is on the W axis at some distance from the original point.
- Any place on the surface of the sphere is equivalent. They are all the same single point, with the radius of the sphere being the distance to the original point.
It’s useful to visualize the W axis as such a spatial object because it drives the idea that there is no escape for the point in the center. Since we are considering a fixed point in 3D, the only thing that can change when we think about its surroundings is the W coordinate. On the other hand these surroundings really are the same in all directions since it is actually a one dimensional axis that we are thinking about. The radius of the sphere is what we use to fold back the visualization to 1D.

Fig. 6. Two points on the W axis.
The outward half-axis
The sphere around the original, fixed point is sitting at a very specific distance from it. This sphere is just a single point along the W axis. Consider one of the tiny eyes looking inward from the surface. Anything behind it is at a larger radius and is further away from the origin, on the W axis.
If we consider the set of all spheres with progressively larger and larger radii, we get half the W axis. By convention let’s associate the inward with the positive direction, and the outward with the negative direction. The expanding sphere starting at the original point is thus the negative half of the W axis.

Fig. 7. The negative W half-axis.
Moving inward
We view the surroundings of the point as the negative half of the W axis. To move forward on the W axis we need to go inside the point.
- Visualize the single, fixed point in 3D space, floating isolated in empty space.
- Shrink yourself close to the point until it appears like a sphere and look inside it.
- In the back of your head, keep in mind that the sphere is still a singular point, it hasn’t really changed size, you have.
- Move slightly inside the sphere so that if you were to look around you would see the original point all around.
- You are now further along the W axis than the original point.
- If you look inward towards the center of the sphere, you are looking into positive W.
This visualization is slightly trickier because we need to turn the pre-existing point into a sphere, while retaining the idea that it’s a point. But it’s the same concept as in the previous visualization.
The best way I’ve found to approach this is that instead of changing the size of the point, I consider that it’s me that is shrunk down very rapidly, and what was previously a point now appears as a bubble, with the forward direction discernible at the center. This helps with the idea that the original point is still sitting at its original coordinate, anchored to the World.
The other worlds on the side
Keep in mind that the original point is fixed at its XYZ coordinate even when we move inside it. This is important because the entire 3D world around is connected to this point. When we move along W in the sequence of concentric spheres, each location we visit is also connected to an entirely new 3D world living on the side.
- Start with the original point in blank XYZ space.
- Flip to the empty space used to reason about the W axis, and visualize the second point outward, as a sphere around it.
- Imagine yourself as growing into a giant, so much that this outer sphere vanishes into a point itself.
- Recall that it still has the other point deep inside it.
- Flip back into XYZ space. The vanished sphere is a point at the origin and we see the usual axes crossing again.
- The 3D world we see from here is not the same as the one around the original, innermost point. We can explore it independently.
Fig. 8. Moving back and forth along the W axis, and exploring the 3D worlds on the side.
The deepness everywhere
Just as we understand that there is a multitude of 3D worlds strung along the W axis, we should realize that such an axis exists at any given location of an XYZ space. It is enriching the concept of space itself, augmenting points neighborhood in the new directions and extending the grand collection of points.
Any lonesome point we picture in a blank emptiness is a window to a perpendicular tunnel going both ways.
This aspect is important to catch insights about spaciousness and density. These last two considerations about worlds on the side and bidirectional tunnels everywhere are just different perspectives to a coherent, dense space.
To wrap the visualization, perform a few loops by going into the fourth axis from one location, emerging in the new 3D world, moving a bit in all three X, Y, Z directions, diving back in the fourth axis, backpedaling, surfacing up in the initial 3D world you started in, and connecting the path to your original location.
Fig. 9. Moving between points in 4D.
Avoiding traps
The main pitfall is to mix up XYZ spatiality with the spatiality of the W axis visualization. This is what is so confusing in the perspective projection, as it completely conflates the two with no way to untangle them. In our case the first step is to be confident with navigating back and forth along W in isolated fashion before attempting to mix them.
The “worlds on the side” can be explored independently as individual, unrelated XYZ spaces, but in a true 4D world there are features and objects that will span a range of W coordinates. It is a mistake to see them as parallel worlds that wouldn’t interact with each other. They are indeed parallel in the mathematical sense, but not really like the parallel worlds of most science fiction. The various realities would not be separate or even merely permeable as in the Stranger Things’ Upside Down. Here, solid objects may span directly across them, in a continuous sense.
When considering segments going diagonally between two 4D coordinates it might be tempting to break them and consider their XYZ and W components separately. Avoid doing this as it will cause trouble later down the road when trying to catch insights about the figures interior vs periphery.
Summary of insights
Here is a summary of the insights we tried to catch:
💡 Orthogonality
The W axis goes into a new direction decoupled from regular 3D space. And goes both ways. When we travel for a bit along the axis we are maintaining our 3D coordinate.
💡 Spaciousness
Every point along the W axis is connected to a new 3D space. Furthermore, the axis is reachable from any given point in a 3D space.
💡 Continuity
There can be objects spanning across the continuum of 3D worlds, laying transversally.
Misplaced concreteness
The only truly important aspect of all the previous paragraphs is the acquisition of the insights by way of thought experiments. The precise technique to reach them isn’t critical. In fact the mental tool must be diluted and attenuated in order for it to be really useful. Taking it too literally will make it too constricting, too physical. The concreteness should be kept as lightweight as possible to limit its own cognitive load and not interfere or compete for thinking resources with the actual subject.
The more you practice, the less concrete it will need to be, and at some point the only thing left from the visualization will be the general abstract idea of “moving” along W in one direction or the other, but all the extra implications gained by the insights will still be attached and help cogitation.
External links
- The World of Blind Mathematicians (2002)
- Alicia Boole Stott, a geometer in higher dimension (2008)
- Flatland - A romance of many dimensions - Edwin A. Abbott (1884)
- Miegakure - How to walk through walls using the 4th Dimension (video) - Excellent insights about orthogonality and continuity.
- Interactive Environment for Intuitive Understanding of 4D object and space - Makoto Murata (2000) - On mapping user controls to 4D actions.
- Shadow-Driven 4D Haptic Visualization - Hui Zhang (2007) - On using haptic feedback to feel 4D objects.
- Visualizing Quaternions - Andrew J. Hanson (2008)
- Hyperbolic VR
- hi.gher.space/forum - Main discussion board on 4D and higher dimensional geometry.